💎

二分木にイテレータを実装してみたら面白かった話

# what to talk

そもそも、イテレータについてよくわかっていない。Rustのイテレータを理解するための方法として、ユーザー定義型に対してイテレータを実装したが、これがよかった。

この発表は、Jim Blandy他(2021)『プログラミングRust 第二版』オライリー・ジャパンの15章におけるBinaryTreeの実装を整理し、再構成したものである。15章とは逆向きに、ユーザー定義型にどう実装するかというところから、イテレータについて学習をしている。

なお、随時、補足を本文中に入れているが、飛ばし読みして構わない。補足は、発表者が理解を整理するために入れたものであったり、この発表でself-containedであることを目指したものだったりする。

# Binary Tree

ここで取り扱うBinary Tree(二分木)は、次のように実装するとする。

Binary Tree(二分木)は以下を満たす構造である:

• 次のいずれかを満たす
  1. 空(Empty)である、
  2. ノードを有しており、ノードは要素、左枝、右枝からなる。さらに左枝と右枝もまたBinaryTreeである
• ノードの要素の型は木全体で一致する。

そして、二分木に要素を追加するところに関するルールとして、

1. 木が空であったら、要素が1つあるだけのノードを持つ木を作り
2. 木が空でない場合、追加する値をノードの要素の値と大小を比較し、
   1. 追加する値がノードの要素の値以下であれば、左の枝に追加する先を探しに行き
   2. 追加する値がノードの要素の値より大きいければ、右の枝に追加する先を探しに行く

。また、二分木には特定の型のものを入れるのではなく、大小比較ができるのであればなんでも入れたい。要素の型については比較可能であるという条件をつけたジェネリック構造体としたい。

例として、以下に二分木を図にしたものを示す。

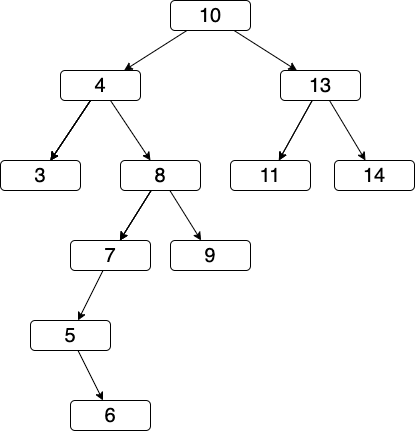
以上をRustのコードにすると以下のようになる。

#[derive(Debug)]
pub enum BinaryTree<T> {
    Empty,
    NonEmpty(Box<TreeNode<T>>),
}

#[derive(Debug)]
pub struct TreeNode<T> {
    pub element: T,
    pub left: BinaryTree<T>,
    pub right: BinaryTree<T>,
}

impl<T: Ord> BinaryTree<T> {
    pub fn add(&mut self, value: T) {
        match *self {
            BinaryTree::Empty => {
                *self = BinaryTree::NonEmpty(Box::new(TreeNode {
                    element: value,
                    left: BinaryTree::Empty,
                    right: BinaryTree::Empty,
                }));
            }
            BinaryTree::NonEmpty(ref mut node) => {
                if value <= node.element {
                    node.left.add(value);
                } else {
                    node.right.add(value);
                }
            }
        }
    }
}

# What is expected in implementing Iterator on BinaryTree

さて、このような二分木に対して、for 文を回した時、どのように値が取り出されることが期待されるか。値が小さい順に出されて欲しい、つまり、左下にあるノードの要素から、順次、上に行き、右枝に行き、右枝でも左下から同じ作業をし、それが尽きたら、上に行く、ということを繰り返していく。

そういったスタックを実装していきたい。画像にすると以下のようになる。

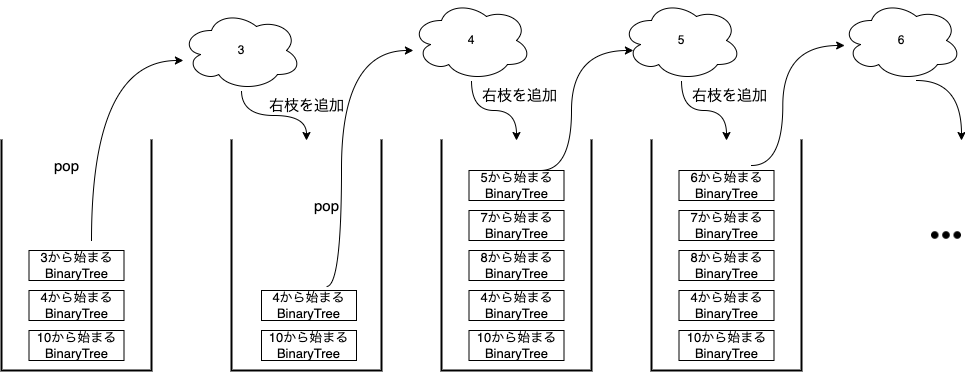
補足

ジェネリック構造体という用語が出たが、これは、構造体にジェネリクスを使うものである。なお、『プログラミングRust第2版』のp.197には「これは、構造体の定義がテンプレートになっていて、任意の型をプラグインできることを意味する。」という記述があるが、ジェネリクスとテンプレートとは別であり、あくまでも比喩表現であることに注意してほしい。

また、impl<T: Ord> BinaryTree<T> {...という記述があったが、これは、

• これはトレイトOrdを実装した任意の型Tについて、
• ジェネリック構造体BinaryTree<T>のメソッドを{...}内で定義すること

を意味する。(なお、Rustにおけるメソッドは構造体定義の中で書くのではなく、別のimplブロックに書く。)

型パラメータ<T: Ord>という記法によって、BinaryTreeのaddの中において、Ordを実装したなんらかの型Tだ、ということが言えるようになる。

トレイト(Trait)、という用語を使っていたが、これは、Rustにおけるインターフェイス、もしくは抽象基底クラスのようなものだ。

なお、トレイトもジェネリクスも多相性(polymorphism)をRustで実現しているものである。しかし、それらがどう違うか、どのように使い分けるかは本発表では扱わない。(アドホック多相性、パラメトリック多相性、サブタイピング多相性が関わる。)

Boxはヒープ上に確保された値であることを示す。

構造体やフィールドにpubをつけていたが、Rustはデフォルトで非公開にしているので、外部からアクセスするために付け加えた。

# Let's implement

前節まではどういうのを実装していきたいかについて記述したが、ここからは具体的にRustでどう実装していくかを見る。

# 実装する理由

我々が目指しているのは、for文をぐるぐる回したら、値が最初から最後まで取れて、終了させられることである。実際にそれを使うのは、おそらくすでにイテレータが実装されている型であれば、あまり考えずに使うことができる。例えば、vというベクタがあって、そのアイテムをプリントする関数を書こうと思ったら次のように書ける。

for element in &v {
    println("{}", element)
}

しかし、これが実際にやっていることは次のように、ベクタをイテレータに変換し、それに対してnext()を呼んで、アイテムが返ってくる限り、printする。

let mut iterator = (&v).into_iter();

while let Some(element) = iterator.next() {
    println("{}", element)
}

自分でイテレータを実装しようと思うと、これらの要素や定型句を理解する必要がる。一つずつ見ていこう。

# Before implementing

イテレータとはそもそも何かと言うことがであるが、これは値の列を生成するもののことを言う。

なお、Rustでの「イテレータ」はトレイトIteratorを実装した任意の型のことであり、「イテレート可能」とはトレイトIntoIteratorを実装した任意の型のこと。何らかのイテレータがあり、かつ、IntoIteratorトレイトを自作の型に対して実装すれば、for文を回せるようになる。

IteratorとIntoIterator、それぞれのTraitは以下の通りである。

pub trait Iterator {
    type Item;
    fn next(&mut self) -> Option<Self::Item>;
}

pub trait IntoIterator {
    type Item;
    type IntoIter: Iterator
    where
        <Self::IntoIter as Iterator>::Item == Self::Item;
    fn into_iter(self) -> Self::IntoIter;
}

補足

説明するに当たって使う用語についていくつか補足していく。

• イテレータが生成する値を「アイテム」と呼ぶ。
• アイテムを受け取るコードを「消費者」と呼ぶ。
• 「アダプタ」は、イテレータを消費し、なんらかの有用な動作を受け取って、別のイテレータを作るものである。
  • mapやfoldとかもアダプタとされる。

# Iterator

次の実装がBinaryTreeをイテレータにする上で本質的である。コレクション型BinaryTreだけではイテレータを実装するには足りず、対応する構造体を定義する必要がある。ここではTreeIterとする。

impl <'a, T: 'a> Iterator for TreeIter<'a, T> {
    type Item = &'a T;

    fn next(&mut self) -> Option<Self::Item> {
        let node = self.unvisited.pop()?;
        self.push_left_edge(&node.right);
        Some(&node.element)
    }

    // ベクタへの変換の実装をするなら、size_hint()を実装したほうがバッファの拡張のコストが下がる。
}

イテレータ、Iteratorを実装している型TreeIterがあり、これがnext()を実装しているから、for文を回せるようになる。

上で掲載した画像からわかるように、処理する順序の管理にはスタックを使うことが期待され、処理がされていないものを上に積んでいくようにしたいので、ベクタでunivisitedをもつ構造体TreeIterを作る。

pub struct TreeIter<'a, T: 'a> {
    unvisited: Vec<&'a TreeNode<T>>
}

そして、TreeIterに対してpush_left_edgeを実装し、根から左枝のを全部スタックに積む関数を実装する。

impl <'a, T: 'a> TreeIter<'a, T> {
    fn push_left_edge(&mut self, mut tree: &'a BinaryTree<T>) {
        while let NonEmpty(ref node) = *tree {
            self.unvisited.push(node);
            tree = &node.left;
        }
    }
}

補足

'aは、ライフタイム(生存期間)を表す(記号の読み方は"tick A"である)。参照の生存期間をRustは気にする。この部分では、TreeIterのelementの型Tのライフタイムは'aであり、それに対してpush_left_edgeの引数となるBinaryTreeの可変参照のライフタイムは'aと一致することを要求している。

# iter()

iter()はコレクション型に対してイテレータを返すメソッドである。そして、iter()で返されるイテレータは個々の要素に対する共有参照を返す。

これにより、コレクションBinaryTreeからイテレータTreeIterを返すメソッドiter()の実装ができる。

impl<T> BinaryTree<T> {
    pub fn iter(&self) -> TreeIter<T> {
        let mut iter = TreeIter { unvisited: Vec::new() };
        iter.push_left_edge(self);
        iter
    }
}

補足

もし繰り返し実行する方法が複数あるなら、iter()を用意せず、それぞれの方法に個別のを用意しましょう。

# IntoIterator

次に、into_ter()を実装する。for文ではこれを呼び出している。これはアイテムへの共有参照を生成するイテレータを返す。

なお、トレイトIntoIteratorを実装している型を、イテレート可能と言う。

impl<'a, T: 'a> IntoIterator for &'a BinaryTree<T> {
    type Item = &'a T;
    type IntoIter = TreeIter<'a, T>;
    fn into_iter(self) -> Self::IntoIter {
        self.iter()
    }
}

補足

iter()は個々のアイテムに対する共有参照を生成するイテレータを返す。iter_mut()は個々のアイテムに対する可変参照を生成するイテレータを返す。(共有参照はリードできる参照であり、複数同時に存在できる。可変参照はライトできる参照であり、可変参照がある時は他に参照は作れない。)

into_iter()は一般に複数実装されており、以下のように実装されている。:

• コレクションの共有参照に対しては、アイテムに対する共有参照を生成するイテレータを返し、
• コレクションの可変参照に対しては、アイテムに対する可変参照を生成するイテレータを返し、
• コレクションの値に対しては、アイテムの所有権を取得し、アイテムを値で返すイテレータを返す。

例えば、以下のように可変参照や所有権の場合に対応した実装をすることができ、&'a mut BinaryTree<T> や BinaryTree<T> に対してもイテレート可能とすることができ、それらを実装することが基本的な御作法である。(なお、発表者は以下の2つを実装しようとしたが、思いつかなかったので諦めた。)

impl<'a, T: 'a> IntoIterator for &'a mut BinaryTree<T> {
// ...
}

impl<T> IntoIterator for BinaryTree<T> {
// ...
}

さて、「コレクション型の共有参照に関して、iterとinto_iter、やっていることが一緒では？」と言う疑問が出るだろう。しかし、以下のような点で異なる。

• into_iterがないとfor文は動かない。
• (&v).into_iter()と書くより、v.iter()と書く方がシンプルであるケースがあるので、コレクションに対してIntoIteratorを実装せずともiter()を実装していることがあり、その場合、iter()は外部のイテレータを返す。
  • Rustのコレクションは大体Iteratorとなる別の構造体を外に用意している背景がある。
  • IntoIteratorでは型をイテレータに変換する方法を指定している。
• IntoIteratorはジェネリックなコードで有用である。
  • T: IntoIteratorとイテレータ可能な型に制約するように書けたり、
  • T: IntoIterator<Item = U>と特定の型Uを生成することを指定できたりする。

# 結果

以上の実装により、BinaryTreeに対してIteratorが実装され、for文でぐるぐる回せたり、mapでやってほしい処理を適用させられるようになった。

    let mut tree = BinaryTree::Empty;
    tree.add("10");
    tree.add("04");
    tree.add("08");
    tree.add("03");
    tree.add("07");
    tree.add("09");
    tree.add("05");
    tree.add("06");
    tree.add("13");
    tree.add("11");
    tree.add("14");

    let mut v = Vec::new();
    for x in &tree {
        v.push(*x);
    }
    assert_eq!(v, vec!["03", "04","05", "06", "07", "08", "09", "10", "11", "13", "14"]);


    let added_prefix = tree.iter().map(|x| format!("number-{}", x)).collect::<Vec<_>>();
    assert_eq!(
        added_prefix,
        vec!["number-03", "number-04", "number-05", "number-06", "number-07", "number-08", "number-09", "number-10", "number-11", "number-13", "number-14"]
    );

# まとめ

ユーザー定義型に対してイテレータを実装する方法は3ステップであった。

1. イテレータを定義する構造体を作る。
2. それに対してIteratorを実装する。
   1. next()を実装する。
3. IntoIteratorを実装する。
   1. into_iter()を実装し、型をイテレート可能にさせる。
4. コレクションのiter()がイテレータを返すようにする。

これだけのことであるが、Rustのイテレータや、いろいろな用語の紹介や補足をしていったら、とんでもなく長くなってしまった。しかし、二分木に対してfor文を回すためにどうするか、と言うところから、Rustのイテレータについての理解や、実際に自分で作ったコレクション型に対してどう実装するかと言う方法について、若干でも助けになったのであれば幸いである。

# おまけ

イテレータ周りはかなり色々あり、語りたいことが多くある(喋りたがりなところについては既に本文を見たらなんとなく感じられただろう)。また、15章には多くのメソッドがあるので、実際にイテレータを使うのならば、ドキュメントを読みながら進めていくことが推奨される。

さて、その中から、いくつかトピックをおまけとして載せておきたくなったので、載せておく。

FromIterator

FromIteratorは実装しなくても困らないが、イテレータでよく使う.collect()での理解にはちょうどよい。.collect()メソッドでは何もベクタにしかイテレータを集めることができないわけではない。

from_iter()を実装していれば、collect()はそれを呼び出し、コレクションにしてくれる。BinaryTreeに対して.addを一つずつ呼び出すのではなく、例えば、ベクタvecがあり、BinaryTree::from_iter(vec.iter().cloned())とすることでBinaryTreeがすぐ作れるようになる。

impl <T: Ord> FromIterator<T> for BinaryTree<T> {
    fn from_iter<I: IntoIterator<Item=T>>(iter: I) -> Self {
        let mut tree = Empty;
        for x in iter {
            tree.add(x);
        }
        tree
    }
}

これにより、以下のようなコードが書けるようになり、楽になる。

let tree = BinaryTree::from_iter(vec.iter().cloned());
let tree2: BinaryTree<i32> = vec.iter().cloned().collect();

なお、アイテムを追加するたびにバッファサイズを追加する可能性があるようなコードは遅くなるので、必要なバッファサイズを事前に確保するように、先にアイテム数の最小値と最大値をわかっていればいい。そのためには、size_hint()メソッドを実装しておくと良い。(今回のBinaryTreeの実装では、先に要素数の最小値はわかるが、最大値はわからない。)

遅延実行

イテレータを受け取って、イテレータを返すのをアダプタと呼ぶ。mapやfilterなどはアイテムに対して何らかの変更を加えているように思えるが、実際のところ、イテレータアダプタは、アイテムを消費せず、新しいイテレータを返すだけである。そして、イテレータを消費するもの(next()やcollect()など)が呼び出されない限り、何も起きない(怠惰であるとも言う)。このように結果が必要になるまで計算を先延ばしにする機構を、遅延実行、と言う。

アキュムレータ

アイテム列全体に対して累積処理を行う汎用処理がある。foldがあるのだが、読む側からすると認知負荷が高いが便利な上に、なぜか関数型言語に慣れている人は好むらしい(参考文献5)ので、紹介する。

foldに対して、第一引数には初期値を入れ、第二引数にクロージャを渡せば、それが簡単に実現できる。

   let tree = BinaryTree::from_iter(vec.iter().cloned());
    assert_eq!(90, tree.iter().fold(0, |n, i| n + i));

rfoldは先頭からではなく、末尾から実行してくれるものであるが、DoubleEndedIteratorを実装していないとできない。

next()のNoneの後の規定

なお、next()を呼び出してNoneが返された後で、さらにnext()を呼び出した場合の規定はない。絶対にNoneを呼びださせたい場合は、fuseアダプタなどを使いましょう。

# 参考文献

1. Jim Blandy他(2021)『プログラミングRust 第二版』オライリー・ジャパン
2. Trait std::iter::Iterator
3. Trait std::iter::IntoIterator
4. Module std::iter - Adapters
5. Processing Arrays non-destructively: for-of vs. .reduce() vs. .flatMap()